MFA

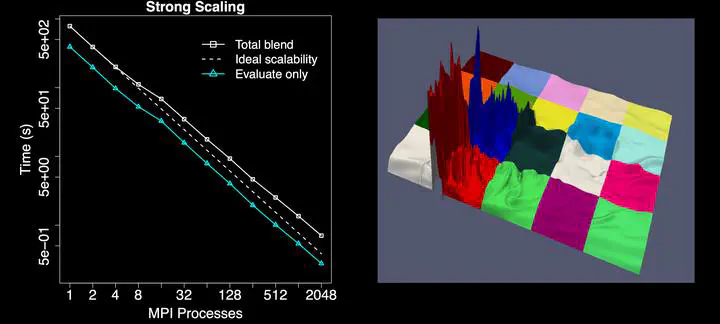
Scientific data may be transformed by recasting to a fundamentally different kind of data model than the discrete point-wise or element-wise datasets produced by computational models. In Multivariate Functional Approximation, or MFA, scientific datasets are redefined in a hypervolume of piecewise-continuous basis functions. Compared with existing discrete models, the continuous functional model can save space while affording many of the same spatiotemporal analyses without reverting back to the discrete form. The MFA model can represent numerous types of data because it is agnostic to the mesh, field, or discretization of the input dataset. Compared with existing discrete data models, the MFA model can enable many spatiotemporal analyses, without converting the entire dataset back to the original discrete form. The MFA often occupies less storage space than the original discrete data, providing some data reduction, depending on data complexity and intended usage. For example, noise may be intentionally smoothed using a small number of control points and high-degree basis functions; alternatively, high-frequency data features may be preserved with more control points and lower degree. Post hoc, the MFA enables analytical closed-form evaluation of points and derivatives, to high order, anywhere inside the domain, without being limited to the locations of the input data points.

Link to MFA Project.